Account Abstraction and the Complex Challenge of Ordering EIP-7702 Transactions

Introduction

Externally owned accounts (EOAs) in Sonic (like in Ethereum) are the most basic accounts and are controlled by a user. Most users interact with EOAs directly, typically through wallets such as Rabby, hardware wallets, etc.

Currently, only EOAs can initiate transactions on Sonic, not smart contracts. The EIP-7702, proposed by Vitalik Buterin et al. and part of Ethereum's Pectra upgrade, introduces a new transaction type that will change this.

Sonic would like to adopt EIP-7702 as it permits account abstraction. Account abstraction overcomes problems like executing batches of transactions and needing a balance to pay transaction fees. Other benefits include defining security rules, recovering lost keys, multi-sigs, gas sponsorship, and custom logic without fully migrating to smart contract logic for EOAs.

The new transaction type of EIP-7702 is challenging for EVM-compatible blockchain implementers like Sonic Labs. One challenge is scheduling transactions in a block with the new transaction type. The proposers of EIP-7702 might not have been fully aware of its computational complexity. This blog reports on this challenge and sketches some proof ideas that scheduling EIP-7702 transactions is an NP-complete problem (NPc), i.e., the solution is hard to find but easy to check.

NP is a class of decision problems for which a solution can be checked in polynomial time, but finding a solution takes exponential time unless P = NP. Whether P equals NP is among the most important open computer science challenges that haven't been solved yet. A wide range of interesting problems in computer science fall into this class and are very hard to solve optimally with current computers since they require an exponential number of computational steps.

Instances of a problem in NPc can be reduced to other problems in NPc. From a computational perspective, they are all equivalent and form a class. If one problem can be solved efficiently, all problems in NPc can be solved efficiently. Such hard problems include finding the longest path in a graph and the traveling salesman problem. The list of NPc problems is very long. The problem is very well illustrated in the book "Computers and Intractability" as a cartoon: A boss calls in an employee in charge of designing and implementing an NPc algorithm. He cannot find an efficient way but has the idea to point the blame at others:

Unfortunately, EIP-7702 introduced a scheduling problem requiring an exponential number of computational steps if we want an optimally ordered transaction list inside a block. In theory, a trade-off between the quality of a schedule and the computation time for the schedule must be found, impacting the throughput of a blockchain either by too many skipped transactions or too much time spent on the schedule construction. This may not be a problem in practice because instances could be straightforward to solve with an efficient and effective heuristic. In any case, better care must be taken between the expressiveness of transactions and their impact on blockchain implementation.

Transaction Scheduling

When a block is constructed in Sonic, transactions are checked to see whether they can be included and where they are placed in the transaction list. Transactions are excluded from a block because the sender's balance has insufficient funds to execute them, the account's nonce does not match the transaction's nonce, and other conditions. We refer to them as "skipped" transactions. One problem is finding a list of transactions for a block so that the number of skipped transactions becomes minimal. In the following discussion, we focus mainly on the nonce.

Let's discuss transactions in more detail. All transactions have a sender (the address account paying for the transaction) and a nonce (a number used once). The latter determines the total order in which transactions of a single sender must be processed. The nonce is initially zero for a new account. Every successful transaction increments the nonce of an account. Also, the transaction itself must reflect the sender's nonce. If the expected nonce of a transaction does not match the sender's nonce, it will be skipped. The nonce mechanism can be seen as a "take a number" ticket machine per account that dispenses numbered tickets for transactions, queuing them, and indicating their place in a queue.

Let (𝑎, 𝑛) denote a transaction sent by the sender address 𝑎 with an expected nonce 𝑛 in the account’s state (an account’s state consists of its balance, nonce, and storage if it's a smart contract). This transaction will not be skipped if executed when the sender’s account 𝑎 has a nonce 𝑛. Suppose we have the following transactions,

(B,1)

(B,2)

(A,1)

(A,2)

(A,3)

which are represented by their senders' addresses and expected nonces. Assume that the nonces of accounts A and B are 1 before executing them. A transaction scheduler seeks a total order for this set of transactions so that the number of skipped transactions is minimal.

There are now many ways to schedule these five transactions (in total, we’ll have 5 * 4 * 3 * 2 * 1 combinations, which equals 120 combinations). A good schedule could be 𝑇 = (𝐵, 1) · (𝐵, 2) · (𝐴, 1) · (𝐴, 2) · (𝐴, 3). If the transactions are executed in this order, we will not experience skipped transaction

However, the schedule 𝑇' = (𝐵, 2) · (𝐴, 3) · (𝐴, 2) · (𝐵, 1) · (𝐴, 1) is sub-optimal because all transactions will be skipped except for (𝐴, 1) and (𝐵, 1). This is because the accounts’ nonces will mismatch with their expected nonces in the transactions

Bad schedules reduce Sonic’s efficiency, and we would like to minimize the number of skipped transactions. Note that without EIP-7702 (like in the previous example), a good schedule can be found by lexicographical sorting, which is computationally efficient.

A New Transaction Type: EIP-7702

EIP-7702 introduces a new transaction type that allows bundling up multiple actions on accounts into a single transaction. In particular, EIP-7702 transactions enable the inclusion of authorizations. The new transaction types have many fields, but we focus only on the sender address, the nonce, and an authorization list for the scheduling discussion.

The list of address nonce pairs (a₀,n₀), (a₁,n₁), ..., (aₖ,nₖ) represents an EIP-7702 transaction where the pair(a₀,n₀) is the sender’s address and its expected nonce, and (a₁,n₁), ..., (aₖ,nₖ) is the authorization list. Each authorization in the authorization list has an address and its expected nonce. The following checks are performed on an EIP-7702 transaction before it can be included in a block:

• The account’s nonce of the sender a₀ is checked; if it does not match the transaction’s nonce n₀, the transaction is skipped.
• If the nonce n₀ matches, the nonce in the sender’s account is incremented, and the authorizations are processed in the given order; for each (aᵢ,nᵢ) for all i, 1 ≤ i ≤ k, if nonce nᵢ matches the account’s nonce, the authorization is accepted, and the nonce is incremented; otherwise, it is ignored.

Crucially, failed authorizations are ignored, and the processing continues. However, the gas price of failed authorizations is still charged to the signer of the overall transaction.

For people familiar with operational semantics, we can formalize the semantics for a given transaction list T = t₁ · t₂ ·...· tₙ and an account’s nonces as a mapping σ: 𝐴 → 𝑁 that maps addresses (from the set of addresses A) to nonces (i.e., natural numbers including zero). The inference rules are shown below.

We have rules for transaction sequences (SEQ), skipped transactions (T-SKIP), and successfully schedulable transactions (T-SUCC). The T-SKIP rule applies if the account's nonce mismatches the transaction's expected nonce. The T-SUCC rule applies if the account's nonce matches the transaction's expected nonce.

The nonces of the authorization and sender addresses are updated in the state σ[a₀ ↦n₀ + 1] before applying the effects of the authorization list. We use an auxiliary function to update the authorizations’ nonces in the authorization list. The auxiliary function δ has two parameters n and a. The authorization updates of the state work as follows: If the state has a matching nonce n for the address a, the nonce in the state is incremented for the address a; otherwise, the state is unchanged. The delta functions are composed with the function composition operator for a compact representation of the T-SUCC rule, which represents a nested function composition, reflecting the nonce changes of a successful EIP-7702 transaction:

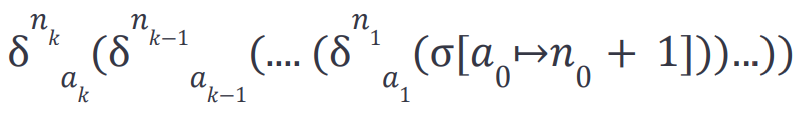
The inference rules provide precise semantics when a transaction is skipped. When ⟨𝑇, σ₀⟩ is evaluated with the inference rules, we will obtain the final state after executing the transactions in the schedule T.  To find the optimal schedule T, we seek a schedule T for a given initial state σ₀ that maximizes the number of successful transactions (or minimizes the number of skipped transactions). We can obtain the number of successful transactions by counting the number of applied T-SUCC rules in the derivation of T.

Alternatively, we can optimize the number of authorizations of a transaction or both objectives simultaneously, making the problem a multi-objective problem. Here, we focus only on maximizing the number of successfully scheduled transactions. 

NP Completeness

The decision problem of the transaction scheduling problem asks whether a schedule  T = t₁ ... tₘ can be found with at least k successful transactions. It is easy to see that an EIP-7702 scheduling problem is in NP since a non-deterministic algorithm needs to guess a schedule (among m! different schedules) and can check the number of successfully scheduled transactions in polynomial time.

To show the hardness of the problem, we take an instance of the longest path problem (the decision version) and reduce it to an instance of the EIP-7702 scheduling problem. A solution of the EIP-7702 gives a solution to the instance of the longest path. If all instances of the longest path problem can be reduced to an instance of the EIP-7702 scheduling problem and solved via EIP-7702, the EIP-7702 scheduling problem is at least as hard as the longest path problem. We know that the longest path problem is an NP-complete problem; hence, the EIP-7702 must be an NP-complete problem since it can be expressed in NP and has the hardness of the longest path problem. 

The longest path problem finds a path of length greater than l in an undirected graph G(V,E) such that a vertex in the graph shows up at most once in the path. We now construct a gadget that translates a graph instance to a list of transactions. By optimally solving the transaction problem, we also have a solution for the longest path problem.

The gadget transcribes the graph G(V,E) into three types of transactions.  We have a vertex transaction tᵤ for each vertex u ∈ V,  an edge transaction tᵤᵥ for each edge (u,v) ∈ E, and a start transaction tₛᵤ for each vertex u ∈ V. A vertex transaction cannot be successfully scheduled before either its start transaction or an incoming edge has been successfully scheduled.  Only one outgoing edge can be successfully scheduled if the vertex transaction of the emanating vertex has been scheduled prior. The basic idea is that the generated successful transactions represent a path walk in the graph with a starting point. The generated path is valid and simple without cycles since we have only one transaction per vertex and vertices can only be connected via an edge. The transaction scheduling problem maximizes the number of successful transactions and, hence, the path length of a path in the graph instance. 

More formally, we introduce a vertex transaction tᵤ = (aᵤ, 1), (a'ᵤ, 0) for each vertex u ∈ V with two unique addresses aᵤ and a'ᵤ. In the initial state σ₀, the nonces of all addresses are zero, and hence, the vertex transactions tᵤ cannot be immediately scheduled without being skipped. It can only be enabled by an edge transaction of an incoming edge or its start transaction.  If successfully scheduled in T, it sets the nonce of the address a'ᵤ to one, enabling one of the edge transactions of an outgoing edge.

For each edge (u,v) ∈ E, we generate new edge transactions tᵤᵥ = (a'ᵤ, 1), (aᵥ, 0) . All outgoing edge transactions of a vertex u compete to be successfully scheduled since they have the same sender address a'ᵤ and the same nonce. Only one can be successfully scheduled, and others must be skipped because the nonce of the address a'ᵤ will be incremented. In addition, they can only be executed after the transaction tᵤ has been scheduled, since its authorization list will contain the address/nonce pair (a'ᵤ, 1). If one of the adjacent-edge transactions is scheduled tᵤᵥ, it will enable the next vertex transaction tᵤ, and so it goes until no further neighboring vertices can be scheduled. Note that the edge relation is symmetric: if (u,v) ∈ E then (v,u) ∈ E since we have a directed graph.

We introduce another set of start transactions tₛᵤ =(aₛ, 0), (aᵤ, 0) for all vertices u ∈ V with a unique address aₛ to find the start of the longest simple path. These transactions are successfully schedulable without any prior transactions. However, only one of the start transactions will be chosen to be successfully scheduled since it has the identical sender address aₛ and nonce of zero. The chosen start transaction will select the first vertex transaction tᵤ because it will increment the nonce of the address aᵤ to one via its authorization.

It is easy to show that the schedule T of the longest path reduction will have the successfully scheduled transactions of the following format by ignoring the skipped transactions, where k is the length of the path and the path is a simple path without cycles.

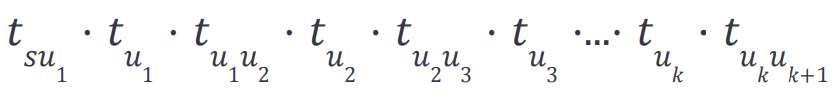
Skipped transactions can be placed arbitrarily in this schedule since they will not influence the nonces (and can be dropped from a reduction’s perspective). Let’s assume we have an optimal solution for EIP-7702. We can provide a YES answer for the longest path instance if we have at least l successfully scheduled vertex transactions; otherwise, we will provide a NO answer. 

Note that the last successful transaction is futile because it cannot connect to a further vertex transaction. I.e., the simple path cannot be further extended by a vertex transaction via a neighbor, assuming we have an optimal schedule (either no neighbor exists anymore, or the neighbors have already been selected).  Sometimes, the last transaction may also not exist if the last node has a single or no neighbors. Consider the following graph with four vertices. 

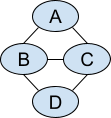
The longest path in the example is not unique. Many longest paths visit all nodes, such as A-B-C-D. We can construct with our gadget the following list of transactions for the vertices:

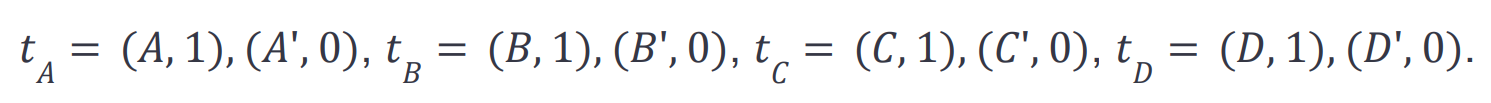
None of them can be scheduled immediately because the nonces of all addresses are set to zero in the initial state. For the adjacent edges of the graph, we have the following transactions,

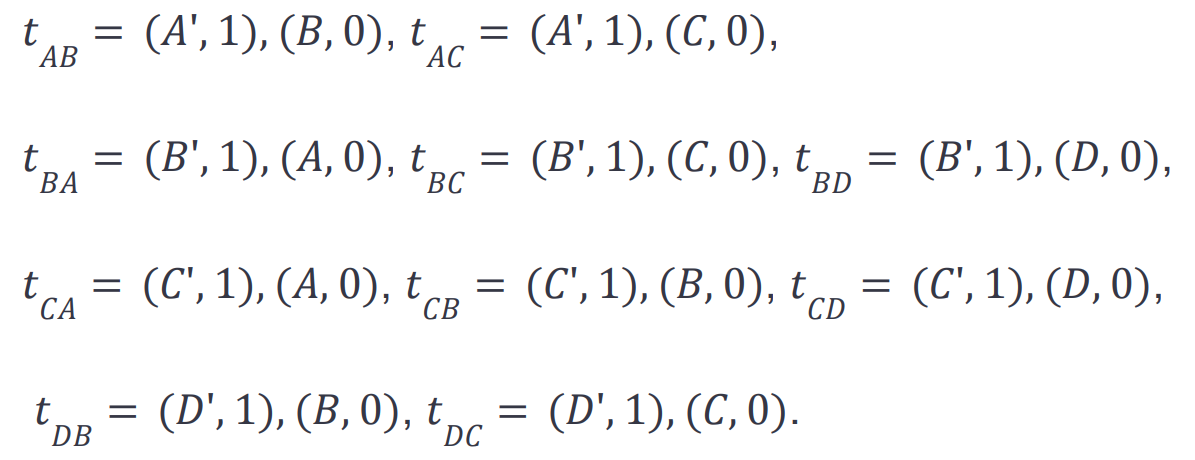
They also cannot be immediately scheduled with the initial state. We have the following list of start transactions:

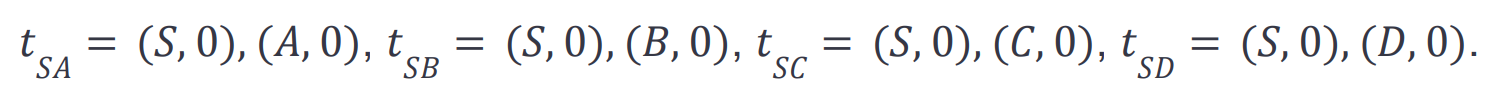
Only one of the transactions can be chosen, as the first successful one will set the nonce of the address S to one.  A possible optimal schedule is where we split the schedule into two sub-schedules for readability: one contains the successfully scheduled transactions, and the other only contains skipped transactions:

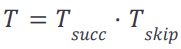
The sub-schedules are as follows:

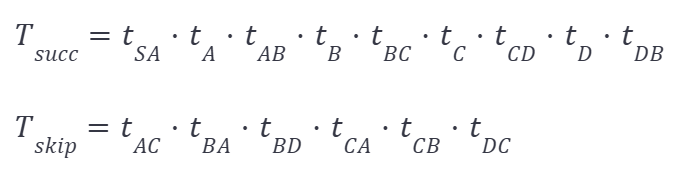
From this schedule, we can deduce the longest path A-B-C-D by listing all the successful vertex transactions in the optimal schedule T in the order of the schedule. Note that all transactions (successful and skipped ones) must be included in the schedule. The provided schedule is only one optimal schedule; many more optimal schedules list a path that visits all nodes in the example.

Summary and What’s Next

Transaction scheduling with EIP-7702 is a very hard problem in computer science. There is no hope of finding an optimal solution unless the computational class of NP problems is equivalent to P (assuming our sketch of the NP reduction is correct). Some people can argue that the input sizes are small and can be brute-forced. We observe that the number of transactions in a block is still large enough, implying unsustainable computational times for optimal schedules. In the literature, there is a phenomenon called phase transition; after a particular problem size/complexity, finding an optimal solution becomes incredibly hard and computationally expensive. 

The chain users must ultimately pay for the computational resources, including the transaction scheduling performed by the validators, making optimal schedules financially unviable and economically inefficient. To overcome this challenge, as a blockchain implementer, we must resort to a scheduling heuristic to overcome the problem's complexity. The heuristic must have a polynomially bounded runtime complexity and deliver sufficiently good schedules to avoid complexity attacks. We will report on our efforts in a future blog.