Formal Verification for DAG Consensus Protocols

TL;DR
Trillions of dollars are locked into blockchains, and hackers may exploit vulnerabilities in them. Thus, key blockchain components must be well-tested before deployment.
However, standard testing/audit techniques are not enough for high levels of assurance. We explore using formal verification to achieve provable security in our blockchain design.
Since the move from proof of work to proof of stake, consensus protocols have become the centerpieces of modern-day blockchains. Consensus protocols must ensure that submitted transactions are eventually included in the ledger and are resilient in the presence of cheating (aka. Byzantine) network nodes.
In addition, consensus must guarantee that all honest nodes in the network eventually construct the same blocks and that their ledgers don’t diverge (thus, exploits like double spending can't occur).
An incorrectly designed consensus protocol will corrupt the blockchain by failing the consistency assumption or showing serious security vulnerabilities. While testing and manual audits may improve the design and code quality, they lack full coverage and mathematical rigor for checking all possible corner cases.
“Program testing can be used to show the presence of bugs, but never to show their absence!”
― Edsger W. Dijkstra ✝
To achieve the highest levels of safety, Sonic Labs has begun deploying formal verification to prove that unsafe behavior is a mathematical impossibility in the Sonic blockchain. Of particular importance is the Sonic consensus protocol. Formal verification uses mathematical/logical proofs that a design, such as a consensus protocol, is functional according to a specification.
Paper and pen proofs will, in most cases, fall short due to the complexity of the protocols and humans' unreliability following through lengthy and complex logical arguments. Instead, semi-automated tools such as a TLA+ proof assistant have been invented to assist in proving computer protocols, including consensus. Even with computer-assisted proofs, the effort required for formally verifying a consensus protocol is costly and time-consuming, but at least not error-prone (the final check is done by the computer, not by humans).
Recently, we developed a proof library in collaboration with logicians from the University of Sydney and INRIA. It contains a family of proofs for DAG-based consensus protocols. DAG-based consensus protocols are robust versions of consensus protocols that share a common data structure (a DAG) between nodes via a broadcast mechanism. We have found that many DAG-based protocols (including Sonic’s consensus) can be verified more efficiently by developing a composition DAG consensus verification library.
The main idea is to pack the complexities of DAG-based protocols into a proof library for safety. For example, if a designer wants to invent a new DAG-based protocol or evolve an existing one. In that case, the library provides models and proofs for its building blocks, and the designer can combine them to describe and prove the new DAG-based protocol.
By exploiting commonalities and compositionality, the effort of modeling new protocols or evolving old ones can be small, especially as protocols evolve. We have made our specifications open source to give back to the blockchain community and make other ecosystems safe.
This work has been presented at the NASA Formal Methods 2025 (NFM 2025) and can be found here. It contains proofs for DAG-Rider, Cordial Miner, Bullshark, Hashgraph, and Aleph, from which we have derived the correctness of other DAG-based protocols, e.g., Sonic consensus.
TLA+ Library
We have developed our verification library in TLA+. Our previous blog explains how to model a simple consensus protocol with TLA+.
To model our protocol, we view it as a state transition system. Each validator runs through this transition system and produces a block. In TLA+, we declare a set of variables that define the state of the transition system.
16 VARIABLES
17 phase_label,
18 blocks_to_propose,
19 proposed_blocks,
20 decided_blocks
21 -------------------------------------------------------------------
Initial(Init) and next (Next) transitions:
22 Init == /\ phase_label = [v \in Validators |-> "receiving"]
23 /\ blocks_to_propose \in [Validators -> Blocks]
24 /\ proposed_blocks = {}
25 /\ decided_blocks = [v \in Validators |-> 0]
26 -------------------------------------------------------------------
41 -------------------------------------------------------------------
42 Next == \E v \in Validators : Propose(v) \/ Decide(v) \/ NextBlock
43 -------------------------------------------------------------------
And lastly, a safety specification: We say that this notion of consistency is a Safety_Invariant.
44 Consistency == \A v1, v2 \in Validators: decided_blocks[v1] # 0 /\ decided_blocks[v2] # 0 => decided_blocks[v1] = decided_blocks[v2]
45 Safety_Invariant == Consistency
46 ===================================================================Given that we have specified the intended behaviour of our system and the properties, we want to find an inductive invariant, i.e. a property that holds initially and is preserved after taking any sequence of valid transitions. Let our inductive invariant be inv, the following conditions should hold:
(1) Init => inv,
(2) inv /\ Next => inv
(3) inv => Safety_Invariant
Typically, we manually work with the theorem prover to suggest a candidate inv by strengthening the Safety_Invariant.
Modular DAG Specifications and Proofs
Unlike the simple consensus protocol, DAG-based protocols, such as Sonic's consensus (described in this blog), require much more complex and intricate specifications and proofs.

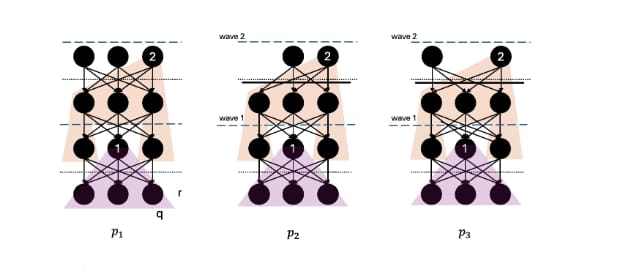
Let us recall some basics of the DAG consensus protocols. As shown in Figure 1, each node (e.g., validator) in the blockchain has a directed acyclic graph (DAG) which is constructed by broadcasts a vertex (also called an event) containing a transaction list.
Moreover, each node receives vertices from other nodes. The sent and received vertices form a DAG where each vertex points to several previous parent vertices. The interpretation of a parent edge is that the transactions in the parent vertices happened before the transactions in the current (child) vertex. However, we need a total order of the vertices to produce a block. As shown in Figure 2, we need anchor vertices that can consistently break symmetry in a partial order across nodes and ensure that a predetermined topological order can be carried out to produce the same block in all nodes.
We call these anchor vertices leaders, and the process of selecting them refers to an election. When a leader vertex is committed (irreversibly elected), we topologically order the vertices from the leader down to the previous leader(s) into a chain of vertices. This chain is then transformed into a block of ordered transactions.
While this general description applies to all DAG protocols, each has nuances. This is summarized among the five popular protocols in Figure 3. For example, protocols like DAG Rider and Aleph rely on a reliable broadcast that guarantees messages will eventually arrive between honest nodes in rounds. In a single round, there is only a single message per node. As a result, equivocation of events cannot occur, which has implications for the election.
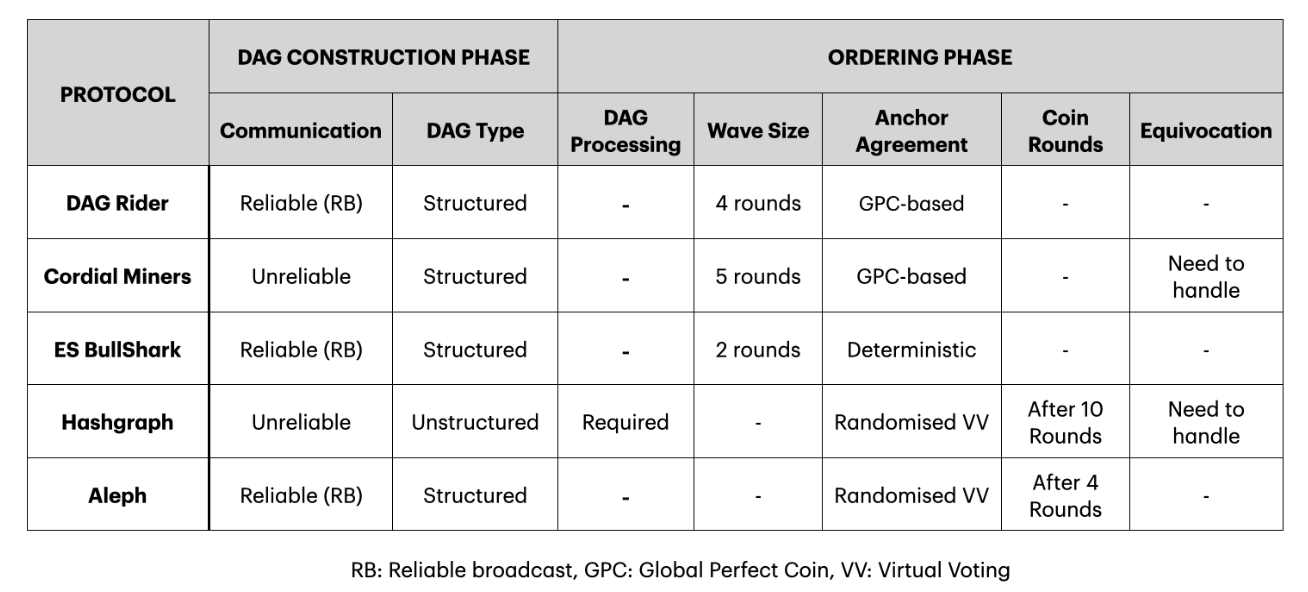
On the other hand, protocols such as cordial miners and Hashgraph use an unreliable broadcast and thus equivocations can occur. Different protocols assume varying network models. For example, DAG Rider and Cordial Miners use a global perfect coin to introduce non-determinism; however, others like Aleph and Hashgraph introduce other forms of randomization.
On the other hand, protocols that have a partial synchronous model do not require nondeterminism. Lastly, the structure of the DAG differs between protocols. Hashgraph, for example, unlike the other protocols, does not block in every round to receive 2f+1 nodes; however, it needs to compute special witness nodes to layer the DAG.
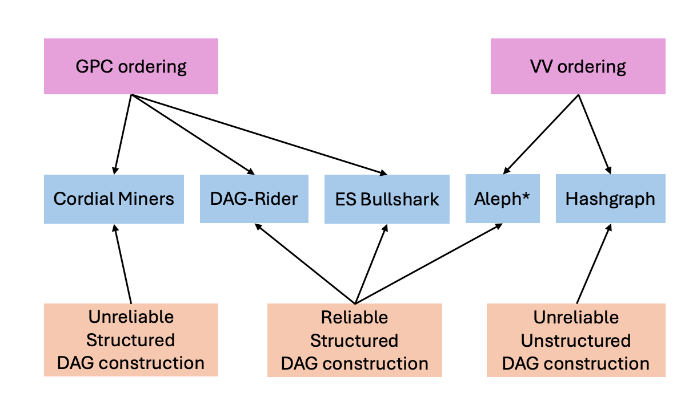
Our verification library has components for DAG construction (orange) and ordering phases (pink). Each abstract component is constructed with a specification and proof, i.e. is individually verified. When these abstract components are combined with a small amount of extra glue code in TLA+, a protocol can be verified compositionally as shown in Figure 4.
For instance, ordering components assumes a consistent DAG. The protocol specifications (blue) specialize in these two components and use their proofs to provide a more refined proof. However, since each component can be verified individually, adding a new protocol requires minimal manual effort and verification time.
Evaluation
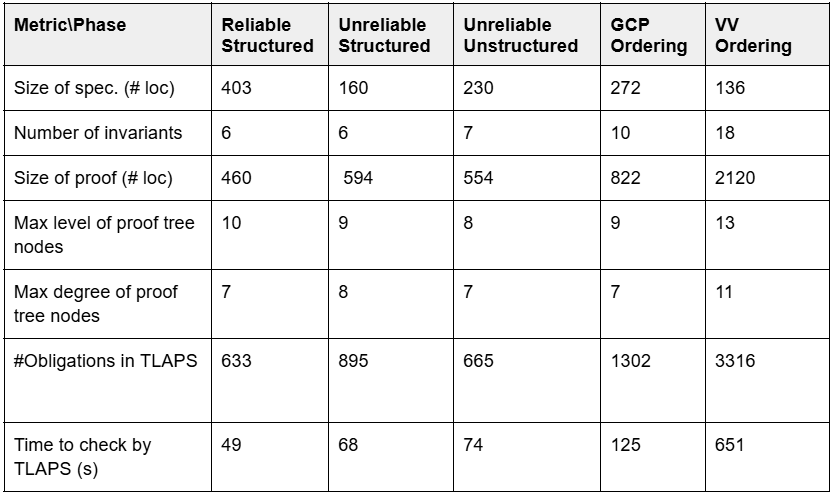
The effort required to understand, define, and validate the five protocols fully spanned approximately 14 person-months distributed among five team members. Formal proof performance was evaluated using TLA+ and TLAPS. Table 1 presents metrics detailing the scope of the DAG construction specifications and the ordering specifications.
Additionally, the table provides metrics regarding proof complexity, including the number of invariants, the size of proof files, the maximum proof depth, the maximum branching within the proof tree structure, and the number of base (leaf) proof obligations. Finally, the table displays the verification time for confirming the safety of each specification.