SonicCS 2.0 — New Consensus for 2x Speed and 68% Memory Reduction

TL;DR
This article presents the new Sonic consensus protocol (SonicCS 2.0). The protocol is a DAG-based consensus protocol that overlaps elections and hence reduces space and computation effort.
Moreover, our algorithm uses 0-1 matrix representations for voting structures to compute elections more efficiently. Experiments on real-world data show that our new protocol has, on average, a 2x speedup and a 68% memory reduction.
Introduction
Sonic is well known for its sub-second time to finality (TTF); a major contributor to this speed is our unique consensus protocol. While our technology already delivers high performance, we continue to improve and enhance it to deliver even greater speed and scalability.
In this article, we’ll delve into our new consensus protocol (SonicCS 2.0), which can incrementally order the transactions of several blocks at every transaction/event update. When run on real-world Sonic transaction data, SonicCS 2.0 has produced, on average, 2x speedups and a 68% memory reduction compared to our previous protocol (SonicCS 1.0).
DAG Consensus Protocols
Let’s recall some basics about the Sonic consensus protocol. Each validator in the blockchain broadcasts an event containing a list of transactions to all other nodes. It also receives event broadcasts from other nodes to itself. The sent and received events are stored in a directed acyclic graph (DAG), also known as a partial order, where each vertex in the DAG is an event that points to several parent events.
The interpretation of a parent is that the transactions in the parent events happened before the transactions in the current (child) event. To produce a block from a DAG, we need to linearize the events into a total order. To do this, we select leader events that consistently break symmetry in the partial order across all nodes. The process of selecting leader events is called an election.
When a leader event is committed (irreversibly elected), we topologically order reachable events from the leader that have not been selected for blocks yet. The events of the topological order form a new block by concatenating the transactions of events to a list of transactions for the new block. We say a protocol is safe if all nodes running the protocol produce the same sequence of blocks. We say a protocol is live if a transaction submitted to the network eventually ends up in the blockchain. Both of these properties need to hold.
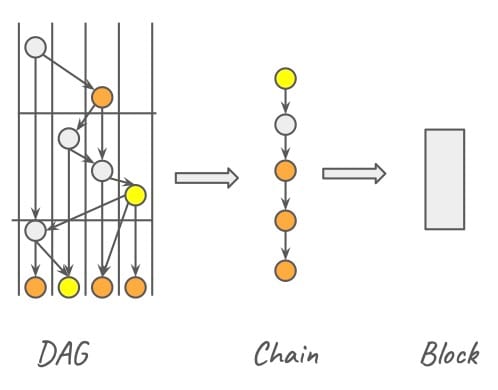
Example: Consider Figure 1. A DAG is shown for a given node. The orange events are candidate leaders, and the yellow events are committed leaders. Events between leaders can be converted to a chain, which allows us to extract a list of transactions to form a block.
Overlapping Election
In Sonic consensus, we assume a layered DAG. Each election has three layers:
- Base layer
- Voting layer
- Aggregation layer
The base layer proposes candidate leaders. The voting layer contains voters who cast a vote if they deem a candidate leader event reachable and honest. The aggregation layer counts each vote and determines if a decision can be made — a quorum of yes or no votes can be aggregated. If it can, it commits the leader. Otherwise, it votes by its majority aggregated value, and the next layer performs aggregation and tries to make a decision.
The obvious way to perform an election is sequentially. For instance, the following is how SonicCS 1.0 performed elections, among several other DAG protocols. First, we perform an election for layer one, layer two votes, layer three aggregates, and so on. When the election is decided, we do the same for layers two, three, and so on. As described in Figure 1, each election produces a block, so the faster the election concludes, the faster the finality of a transaction in the blockchain.
However, a key observation is that an event can be both a base layer, a voting layer, and an aggregation layer in different elections. Thus, we exploit this fact to overlap elections, and when a new event arrives, we check if it’s an aggregator, a voter, or a leader candidate. For any of these roles, it can perform all its duties concurrently for several elections.
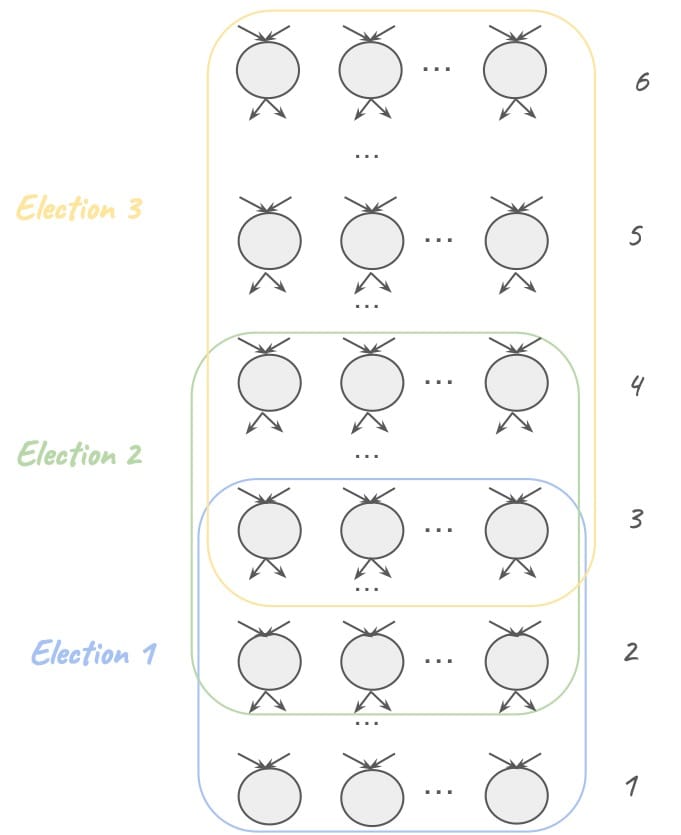
Example: Consider Figure 2. Elections 1 (blue), 2 (green), and 3 (yellow) can overlap since selected events in layer two can be both candidates and voters, and selected events in layers 3 and 4 can be candidates, voters, and aggregators in different elections.
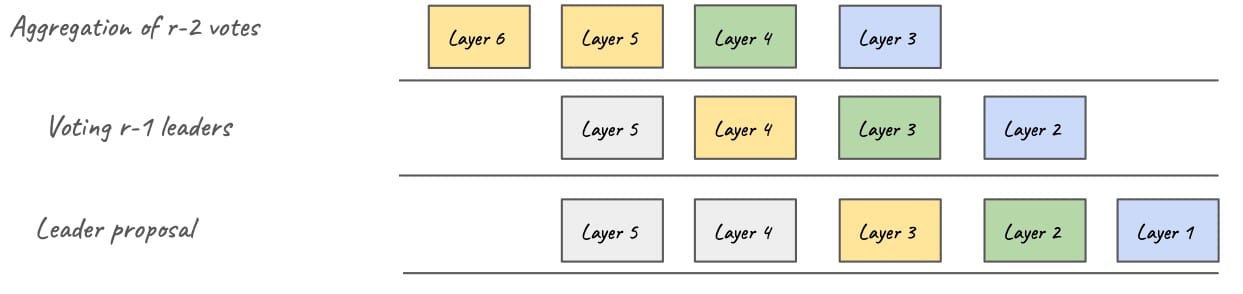
An alternative view of our approach is to see each layer as a process and the overlapping elections as a pipeline of actions, as shown in Figure 3.
Vectorization
Overlapping elections naturally lead to parallelization opportunities. To this end, we’ve further redesigned the election implementation to leverage an election's inductive nature to optimize both storage and computation.
Instead of individually performing each vote and subsequent aggregation, we observe that the number of validators and their stakes are fixed and known at the beginning of each epoch. Thus, each voting event is associated with a matrix depicted in Figure 4, where one dimension of the matrix is the layers that an event can vote/aggregate on, and the other one is the set of validators.
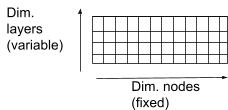
While the nodes’ dimension remains fixed for all events, the layers’ dimension varies depending on the layer of the event and its progress with voting. For instance, a layer two event will have a single vector, i.e., a 1x|Node| matrix, as this event can only vote for a layer one candidate and can’t aggregate. On the other hand, an event belonging to layer two will have a 2x|Nodes| matrix to hold votes for events in layers one and two.
Note that before putting in final votes for layers eligible for aggregation (which are to be built upon by following frame roots if not decided), we test those rows for criteria of reaching a decision. Aggregating the votes requires multiplying each row of each event matrix and adding the matrices together (element-wise). After aggregation, an additional row of votes is added by each event to represent the votes for events one layer below itself.
Besides being inherently more succinct, such voting structures allow the vectorization of their operations (matrix scaling and addition) using CPU SIMD instructions. We implement our algorithm to use these more efficient instructions (specifically AVX2, as it’s the most common) if they’re available on the host machine (and default to a software solution otherwise).
Performance
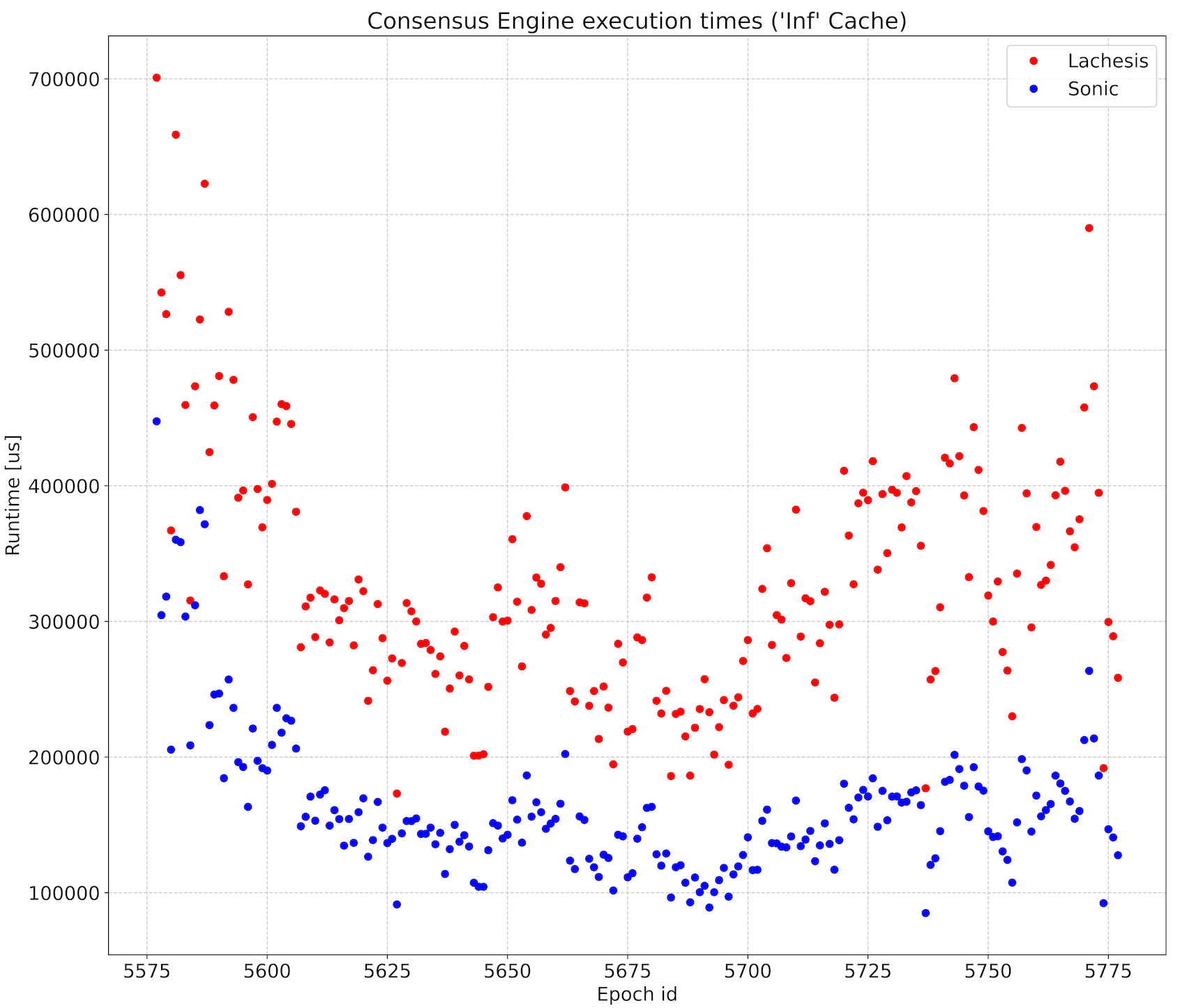
We performed preliminary experiments and compared the execution times of SonicCS 2.0 to SonicCS 1.0. We used 200 epochs of transactions from the Sonic mainnet for the data. On average, the new consensus protocol exhibits a speedup of 2.04x with a minimum of 1.37x and a maximum of 2.62x.
We note that the new consensus is never slower than SonicCS 1.0. Moreover, SonicCS 2.0 uses only 135 megabytes per epoch, down from 420 megabytes per epoch in SonicCS 1.0. This constitutes a 68% reduction in memory per epoch.
Conclusion
We've presented SonicCS 2.0, our new consensus protocol that, among other improvements, exploits the fact that elections can overlap. Our preliminary experiments on 200 epochs in the Sonic mainnet have shown a 2x speedup (on average) and memory reductions of 68%.
We aim to include the protocol in one of the Sonic client’s next releases and will follow up on this article with a detailed technical report shortly.



